Découverte des primitives de dessin 3D d'OpenSCAD

Présentation et objectifs

Ce tutoriel a pour but de faire découvrir les primitives de dessin 3D du langage OpenSCAD. Il vous permettra d'apprendre à utiliser les primitives suivantes :

• sphere()
• cube()
• cylinder()
• polyhedron()

Comme pour le dessin 2D, le nombre de primitives en 3D est assez faible. Chacune d'entre elles aura plusieurs utilisations possibles.

Pré-requis

Avant de faire ce tutoriel, il faut comprendre la logique d'utilisation d'OpenSCAD. Si vous n'avez jamais ouvert ce logiciel, vous pouvez suivre le tutoriel suivant :

• Premier pas avec OpenSCAD.

Découverte des primitives de dessin 3D

Première primitive : sphere()

La primitive sphere() dessine comme son nom l'indique une sphère dont le paramètre $r$ est le rayon. Contrairement aux autres figures rencontrées jusqu'à maintenant, la sphère est toujours centrée.

sphere(r | d=diameter)

Ci-dessous, quelques exemples d'utilisation de la cette primitive à expérimenter pour mieux comprendre ses possibilités :

sphere(r = 1);
sphere(r = 5);
sphere(r = 10);
sphere(d = 2);
sphere(d = 10);
sphere(d = 20);
sphere(100, $fn=3);
sphere(100, $fn=6);
sphere(100, $fn=8); 
sphere(100, $fn=360);

Deuxième primitive : cube()

La primitive cube() dessine un parallélépipède. S’il s’agit d’un cube il suffit de ne préciser qu’une dimension sans crochets droits.

cube(size, center = false)
cube([width,depth,height])

Par exemple, pour tester les trois types d'appels possible de cette commande, vous pouvez essayez ces différentes commandes les unes après les autres :

cube(30);
cube (size=10, center=true);
cube ([5,10,15]);

Troisième primitive : cylinder()

La primitive cylinder() permet de dessiner principalement des cylindres, avec le paramètre r indiquant son rayon. Elle est en réalité plus générique que ça en permettant de dessiner d'autres polyèdres de révolution comme les cônes ou les tronc de cônes. Dans ce cas là, les paramètres r1 et r2 indique les deux rayons ( bas et haut). Pour toutes ces figures, h détermine la hauteur. Le paramètre $fn peut être précisé pour indiquer le nombre de faces.

cylinder(h,r|d,center) 
cylinder(h,r1|d1,r2|d2,center)

Ci-dessous, quelques exemples d'utilisation de la cette primitive à expérimenter pour mieux comprendre ses possibilités :

cylinder(h = 10, r=20);
cylinder(h = 10, r=20, $fn=6);
cylinder(h = 10, r1 = 10, r2 = 20, center = false);
cylinder(h = 10, r1 = 20, r2 = 10, center = true);
cylinder(h = 10, d=40);
cylinder(h = 10, d=40, $fn=6);
cylinder(h = 10, d1 = 20, d2 = 40, center = false);
cylinder(h = 10, d1 = 40, d2 = 20, center = true);

Quatrième primitive : polyhedron()

Cette dernière primitive est la plus complexe de toute. Elle permet de dessiner un polyèdre quelconque en spécifiant chacune de ses faces. Les faces seront découpées en triangle.

Le paramètre points énumère la liste des sommets du poly­èdre, chaque sommet étant décrit par un triplet de coordonnées X, Y et Z. Le second paramètre triangles décrit chaque triangle composant la surface, en indiquant ses trois sommets. Il s’agit là aussi d’une suite de triplets dont chacun désigne, trois des sommets indiqués dans la liste des sommets points. Par exemple dans triangles, un triplet [0,3,2] désignera les 1er, 4e et 3e triplets (donc sommets) contenus dans points.

polyhedron(points, triangles)

Par exemple, pour dessiner un cube avec cette primitive, il faut écrire le code suivant :

polyhedron(
points = [[-10,-10,0], [-10,10,0], 
          [10,10,0], [10,-10,0],
          [-10,-10,20],[-10,10,20],
          [10,10,20],[10,-10,20]],
triangles = [[0,4,7], [3,0,7],  // face avant
             [0,1,5], [4,0,5],  // face gauche
             [3,7,6], [2,3,6],  // face droite
             [5,1,6], [1,2,6],  // face arrière
             [1,0,2], [0,3,2],  // bas
             [4,5,6], [7,4,6]]  // haut
);

Cette primitive est la plus puissante de toute mais aussi la plus difficile à maitriser. Généralement on essaye autant que possible de s'en passer lorsque c'est possible.

Un autre exemple de polyèdre plus complexe :

polyhedron(
points = [[0, -10, 60], 
          [0, 10, 60], 
          [0, 10, 0], 
          [0, -10, 0], 
          [60, -10, 60], 
          [60, 10, 60], 
	      [10, -10, 50], 
          [10, 10, 50], 
          [10, 10, 30], 
          [10, -10, 30], 
          [30, -10, 50], 
          [30, 10, 50]], 
faces = [[0,3,2], [0,2,1], 
         [4,0,5], [5,0,1],
         [5,2,4], [4,2,3],
         [6,8,9], [6,7,8],
         [6,10,11], [6,11,7], 
         [10,8,11], [10,9,8], 
         [3,0,9], [9,0,6],  
         [10,6, 0], [0,4,10],
         [3,9,10], [3,10,4], 
         [1,7,11], [1,11,5],
         [1,8,7], [2,8,1],
         [8,2,11], [5,11,2]]
);

Ce code une fois compilé (F5) produira le modèle suivant :

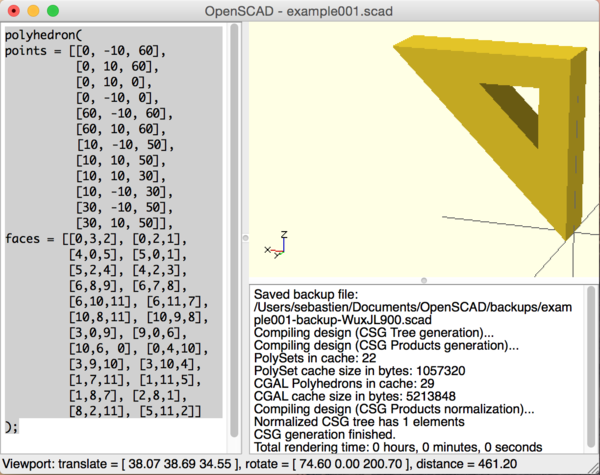
Pour aller plus loin

L'ensemble de ses primitives permet de démarrer la modélisation. Sans les opérations ensemblistes, les possibilités sont encore limitées.

Bibliographie

• Primitive 3D
• Tutoriel RepRapide