Random Shield
Sommaire
Présentation du projet
Générateur de bits aléatoires pour Arduino
- Permet de générer des bits aléatoires pour des applications ludiques ou cryptographiques
- Circuit simple à mettre en oeuvre
- Nécessite deux piles 9V ou une alimentation symétrique 12V
- Vitesse d'acquisition max de 6.25 kbits par seconde
Circuit de base
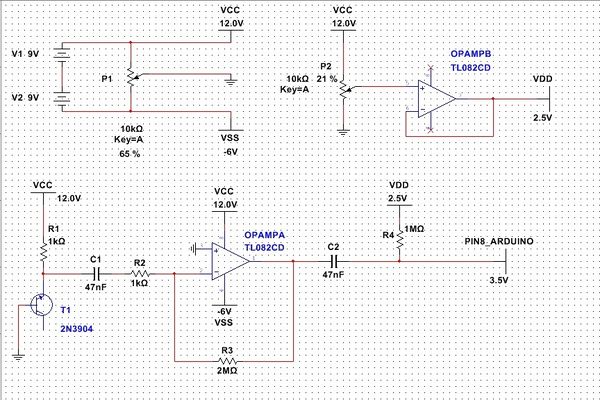
Principe de fonctionnement
On génère du bruit en se plaçant dans la zone de tension inverse d'une diode zener ou d'une jonction PN en inverse d'un transistor. On assiste alors à un effet d'avalanche, où les électrons vont se mouvoir de manière complètement aléatoire. On utilise ici un 2N3904 car sa tension inverse n'est pas très élevée (8.2V) et le bruit qu'il génère possède une grande amplitude.
On amplifie le signal obtenu à travers un AOP, mais en faisant d'abord passer le signal à travers un condensateur. Ceci permet d'éliminer la tension d'offset (la tension inverse) de 8.2V. Noter que le schéma d'alimentation avec les deux piles n'est pas symétrique : on se met en +12V justement pour être bien au-dessus de la tension d'avalanche.
On amplifie le signal de telle sorte qu'on ait une amplitude de 4V peak to peak (il évolue entre +2V et -2V pour l'instant).
Note : J'avais mesuré un bruit de 90mV à la sortie de C1, mais j'ai découvert qu'il fallait une résistance de 2Mohms sur le feedback de l'AOP, soit un gain de 2000. Je devrais alors avoir en théorie un signal de sortie de 180V peak to peak !!! Mystère encore à ce jour ... Mais bon, vu que ça marche bien comme ça ... :-)
A la sortie de l'AOP, on place encore un autre condensateur afin de pouvoir mettre une tension d'offset sur le signal amplifié. En effet, la logique de l'Arduino est : logique 0 : 0-0.9V et logique 1 : 3V-4.2V. Il faut donc que le signal soit bien ajusté dans cette bande. Par expérience, j'ai trouvé qu'il faut régler le potentiomètre P2 à 2.5V.
Note : Au fur et à mesure que les piles 9V se déchargent, il sera probablement nécessaire de réajuster le potentiomètre P1 pour qu'on ait bien +12V. La valeur de la tension négative importe peu, du moment, qu'on ait -3V minimum pour assurer l'amplification correcte du signal. Il faudra également vérifier que P2 délivre 2.5V.
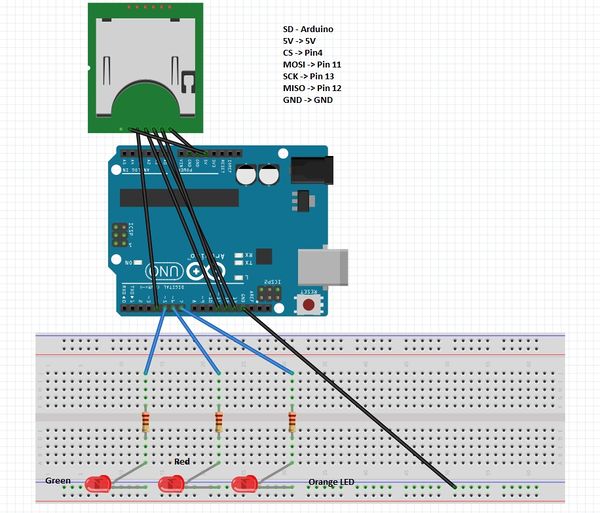
Code Arduino
// Basic program that acquires the noise bits as fast as possible
// Led interface for status report
// One bit per byte in the SD file
// 6.25 kbits per second max
// Claude Jaspart claude.a.jaspart@gmail.com - June 2015
#include <SPI.h>
#include <SD.h>
File myFile;
int RNG_signal = 8; // The signal of the shield is on this pin
int ledwait = 7; // This led will indicate the init phase of the program
// If ledwait turns on at the same as ledack, then the SD card couldn't be init
int ledacq=6; // This led will indicate that the Arduino is acquiring bits
int ledok=5; // This led will indicate that the Arduino has finishing acquiring the bits and the SD card can be removed
unsigned int RNG_bit = 0; // The value of the read bit from the signal will be stored here
unsigned int counter = 0; // Used for determining how many bits have been read so far
const unsigned int max_count = 50000; // Max value could be 65535, but simple to count in blocks of 50kbits
unsigned int repeat = 1; // Used for determining how many bits have been read so far
const unsigned int max_repeat = 20; // size of sample = max_count * max_repeat, here 20 * 50000 = 1 Mbits
unsigned int sample_microsecs = 500; // If you want to read bits at a particular rate, 500 microsecs min value
void setup()
{
// Defining the digital pins for the signal and leds
pinMode(RNG_signal, INPUT);
pinMode(ledwait, OUTPUT);
pinMode(ledacq, OUTPUT);
pinMode(ledok, OUTPUT);
// Init of the leds
digitalWrite(ledwait, LOW);
digitalWrite(ledacq, LOW);
digitalWrite(ledok, LOW);
// Starting the init phase
digitalWrite(ledwait, HIGH);
// Init the SD card
if (!SD.begin(4))
{
digitalWrite(ledacq, HIGH);
digitalWrite(ledwait, HIGH);
return;
}
// Creating the file
myFile = SD.open("rng.txt", FILE_WRITE);
// Going to the Acq phase
delay(2000);
digitalWrite(ledwait, LOW);
digitalWrite(ledacq, HIGH);
}
void loop()
{
// Reading the signal bit and writing it to the file
RNG_bit = digitalRead(RNG_signal);
myFile.print(RNG_bit);
// Block that determines how many bits have been read
counter++;
if ( counter >= max_count )
{
if (repeat >= max_repeat)
{
myFile.close();
digitalWrite(ledacq, LOW);
digitalWrite(ledok, HIGH);
while(1);
}
else
{
repeat++;
counter = 0;
}
}
// If you want to acquire bits at a given rate (min 500microsecs)
//delayMicroseconds(time_sample_microsecs);
}
Test du générateur
Il n'existe aucune méthode fiable pour déterminer si une suite de nombre est aléatoire. On ne peut que vérifier si le générateur se comporte "normalement" d'un point de vue statistique.
J'ai installé la batterie de test connue sous le nom DieHarder :
terminal:sudo apt-get install dieharder
Pour lancer les tests, rien de plus simple (ici sur un échantillon de 2 mégabits) :
terminal:dieharder -f rng.txt -a
Voici le résultat :
#=============================================================================#
# dieharder version 3.31.1 Copyright 2003 Robert G. Brown #
#=============================================================================#
rng_name | filename |rands/second|
mt19937| RNG.TXT| 1.29e+08 |
#=============================================================================#
test_name |ntup| tsamples |psamples| p-value |Assessment
#=============================================================================#
diehard_birthdays| 0| 100| 100|0.30889575| PASSED
diehard_operm5| 0| 1000000| 100|0.99081369| PASSED
diehard_rank_32x32| 0| 40000| 100|0.79546934| PASSED
diehard_rank_6x8| 0| 100000| 100|0.90281704| PASSED
diehard_bitstream| 0| 2097152| 100|0.86512718| PASSED
diehard_opso| 0| 2097152| 100|0.31791348| PASSED
diehard_oqso| 0| 2097152| 100|0.53248615| PASSED
diehard_dna| 0| 2097152| 100|0.78644034| PASSED
diehard_count_1s_str| 0| 256000| 100|0.90216600| PASSED
diehard_count_1s_byt| 0| 256000| 100|0.57958785| PASSED
diehard_parking_lot| 0| 12000| 100|0.45123033| PASSED
diehard_2dsphere| 2| 8000| 100|0.07839664| PASSED
diehard_3dsphere| 3| 4000| 100|0.76106594| PASSED
diehard_squeeze| 0| 100000| 100|0.02475387| PASSED
diehard_sums| 0| 100| 100|0.16259036| PASSED
diehard_runs| 0| 100000| 100|0.12672226| PASSED
diehard_runs| 0| 100000| 100|0.42649685| PASSED
diehard_craps| 0| 200000| 100|0.37205173| PASSED
diehard_craps| 0| 200000| 100|0.78931850| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.73730273| PASSED
marsaglia_tsang_gcd| 0| 10000000| 100|0.83482357| PASSED
sts_monobit| 1| 100000| 100|0.72618254| PASSED
sts_runs| 2| 100000| 100|0.89478484| PASSED
sts_serial| 1| 100000| 100|0.13273684| PASSED
sts_serial| 2| 100000| 100|0.60467750| PASSED
sts_serial| 3| 100000| 100|0.36788816| PASSED
sts_serial| 3| 100000| 100|0.45945882| PASSED
sts_serial| 4| 100000| 100|0.52089161| PASSED
sts_serial| 4| 100000| 100|0.50654753| PASSED
sts_serial| 5| 100000| 100|0.64402415| PASSED
sts_serial| 5| 100000| 100|0.90261034| PASSED
sts_serial| 6| 100000| 100|0.54809205| PASSED
sts_serial| 6| 100000| 100|0.53676669| PASSED
sts_serial| 7| 100000| 100|0.07964161| PASSED
sts_serial| 7| 100000| 100|0.04039882| PASSED
sts_serial| 8| 100000| 100|0.12819180| PASSED
sts_serial| 8| 100000| 100|0.98790885| PASSED
sts_serial| 9| 100000| 100|0.13273201| PASSED
sts_serial| 9| 100000| 100|0.35787029| PASSED
sts_serial| 10| 100000| 100|0.82298480| PASSED
sts_serial| 10| 100000| 100|0.97802272| PASSED
sts_serial| 11| 100000| 100|0.87189101| PASSED
sts_serial| 11| 100000| 100|0.65033244| PASSED
sts_serial| 12| 100000| 100|0.93100183| PASSED
sts_serial| 12| 100000| 100|0.99869428| WEAK
sts_serial| 13| 100000| 100|0.99646843| WEAK
sts_serial| 13| 100000| 100|0.40432078| PASSED
sts_serial| 14| 100000| 100|0.71285726| PASSED
sts_serial| 14| 100000| 100|0.31898898| PASSED
sts_serial| 15| 100000| 100|0.88309583| PASSED
sts_serial| 15| 100000| 100|0.95643787| PASSED
sts_serial| 16| 100000| 100|0.89957361| PASSED
sts_serial| 16| 100000| 100|0.96772499| PASSED
rgb_bitdist| 1| 100000| 100|0.95623079| PASSED
rgb_bitdist| 2| 100000| 100|0.58789918| PASSED
rgb_bitdist| 3| 100000| 100|0.95440344| PASSED
rgb_bitdist| 4| 100000| 100|0.98258544| PASSED
rgb_bitdist| 5| 100000| 100|0.08135261| PASSED
rgb_bitdist| 6| 100000| 100|0.92614458| PASSED
rgb_bitdist| 7| 100000| 100|0.99177385| PASSED
rgb_bitdist| 8| 100000| 100|0.99188216| PASSED
rgb_bitdist| 9| 100000| 100|0.97692511| PASSED
rgb_bitdist| 10| 100000| 100|0.47151755| PASSED
rgb_bitdist| 11| 100000| 100|0.59783413| PASSED
rgb_bitdist| 12| 100000| 100|0.19750764| PASSED
rgb_minimum_distance| 2| 10000| 1000|0.27194018| PASSED
rgb_minimum_distance| 3| 10000| 1000|0.28712170| PASSED
rgb_minimum_distance| 4| 10000| 1000|0.65299684| PASSED
rgb_minimum_distance| 5| 10000| 1000|0.12188697| PASSED
rgb_permutations| 2| 100000| 100|0.56273791| PASSED
rgb_permutations| 3| 100000| 100|0.64514608| PASSED
rgb_permutations| 4| 100000| 100|0.31960630| PASSED
rgb_permutations| 5| 100000| 100|0.84713061| PASSED
rgb_lagged_sum| 0| 1000000| 100|0.88527221| PASSED
rgb_lagged_sum| 1| 1000000| 100|0.99152865| PASSED
rgb_lagged_sum| 2| 1000000| 100|0.07103505| PASSED
rgb_lagged_sum| 3| 1000000| 100|0.07072667| PASSED
rgb_lagged_sum| 4| 1000000| 100|0.06759505| PASSED
rgb_lagged_sum| 5| 1000000| 100|0.24333290| PASSED
rgb_lagged_sum| 6| 1000000| 100|0.13992249| PASSED
rgb_lagged_sum| 7| 1000000| 100|0.50312525| PASSED
rgb_lagged_sum| 8| 1000000| 100|0.11746691| PASSED
rgb_lagged_sum| 9| 1000000| 100|0.45940744| PASSED
rgb_lagged_sum| 10| 1000000| 100|0.39016408| PASSED
rgb_lagged_sum| 11| 1000000| 100|0.65350506| PASSED
rgb_lagged_sum| 12| 1000000| 100|0.99241243| PASSED
rgb_lagged_sum| 13| 1000000| 100|0.05774255| PASSED
rgb_lagged_sum| 14| 1000000| 100|0.35248899| PASSED
rgb_lagged_sum| 15| 1000000| 100|0.34204029| PASSED
rgb_lagged_sum| 16| 1000000| 100|0.26109225| PASSED
rgb_lagged_sum| 17| 1000000| 100|0.25001244| PASSED
rgb_lagged_sum| 18| 1000000| 100|0.08612312| PASSED
rgb_lagged_sum| 19| 1000000| 100|0.67709116| PASSED
rgb_lagged_sum| 20| 1000000| 100|0.19598901| PASSED
rgb_lagged_sum| 21| 1000000| 100|0.58653101| PASSED
rgb_lagged_sum| 22| 1000000| 100|0.54480996| PASSED
rgb_lagged_sum| 23| 1000000| 100|0.97657972| PASSED
rgb_lagged_sum| 24| 1000000| 100|0.06151635| PASSED
rgb_lagged_sum| 25| 1000000| 100|0.69753975| PASSED
rgb_lagged_sum| 26| 1000000| 100|0.44499540| PASSED
rgb_lagged_sum| 27| 1000000| 100|0.85393902| PASSED
rgb_lagged_sum| 28| 1000000| 100|0.17044719| PASSED
rgb_lagged_sum| 29| 1000000| 100|0.98515748| PASSED
rgb_lagged_sum| 30| 1000000| 100|0.92187461| PASSED
rgb_lagged_sum| 31| 1000000| 100|0.62877226| PASSED
rgb_lagged_sum| 32| 1000000| 100|0.99398180| PASSED
rgb_kstest_test| 0| 10000| 1000|0.00510267| PASSED
dab_bytedistrib| 0| 51200000| 1|0.96033595| PASSED
dab_dct| 256| 50000| 1|0.74894574| PASSED
Preparing to run test 207. ntuple = 0
dab_filltree| 32| 15000000| 1|0.61815623| PASSED
dab_filltree| 32| 15000000| 1|0.11110069| PASSED
Preparing to run test 208. ntuple = 0
dab_filltree2| 0| 5000000| 1|0.69384760| PASSED
dab_filltree2| 1| 5000000| 1|0.87581645| PASSED
Preparing to run test 209. ntuple = 0
dab_monobit2| 12| 65000000| 1|0.58191574| PASSED
A part deux instances où le test a échoué, je me sens très confiant dans l'efficacité du générateur.
Evolution du projet
- Boitier de rangement
- Compresser 8 random bits sur 1 byte
- Interface graphique avec menus et potentiomètre/boutons poussoirs pour faire la sélection
- Interface bluetooth pour connection avec un smartphone
- Générer et afficher en gros sur l'écran un ou plusieurs nombres aléatoires (pour remplacer les dés)
- Deuxième carte SD pour l'application cryptographique One Time Pad
Références
http://holdenc.altervista.org/avalanche/
https://www.random.org/